.ipynb .pdf

Repository offenes Thema

Binder Live Code

Inhalt

Propagation of a light pulse in a dispersive medium

In this exercise we will solve the time evolution of a light pulse. We will describe its initial shape by function $A(z,t=0)$, which is assumed to be Gaussian for simplicity:

$$A(z,t=0)=e^{-z^2/2{\sigma }^2}{e}^{i{k}_{0}z}$$

In plots etc, we will always only work with the real part of the wave package.

import numpy as np
import matplotlib.pyplot as plt

A quick initial plot.

# properties of the wave package
sigmaz = 2
k0 = 5

# parameters for plotting
Nz = 512
zmax = 7.5

zlin = np.linspace(-zmax, zmax, Nz)
Az = np.exp(-zlin**2/2/sigmaz**2)*np.exp(1j*k0*zlin)
Aenv = np.exp(-zlin**2/2/sigmaz**2)

f, ax = plt.subplots()
ax.plot(zlin, Az.real, label = 'electric field');
ax.plot(zlin, Aenv, 'r', ls = '--', label='envelope');
ax.set_xlabel('position $z$[L]');
ax.set_ylabel(' $\mathcal{Re}(A)$');
ax.legend()

<matplotlib.legend.Legend at 0x10f3a09a0>

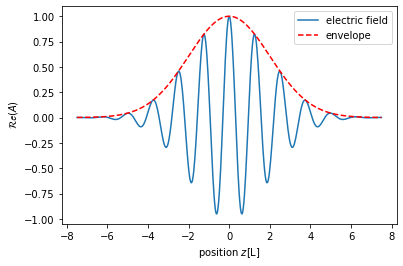
We would now like to understand, how this wave-package propagates. In a non-linear medium the propagation is not easily solved, but we have to know the dispersion relationship of the medium. In our case, we will use the relationship:

$$\omega (k)=k_0{v}_p+(k-k_0)v_g+\frac{\mathrm{\Gamma }}{2}(k-k_0{)}^2$$

For each single wavelength $k$, we then know the time evolution of the wave package to be:

$$a(k,t)=a(k,t=0)e^{-i\omega (k)t}$$

And the full time evolution is then obtain through the Fourier transform

$$A(z,t)=\int dk{e}^{ikz}a(k,t)$$

The intial wavepackage in Fourier space

As we know $A(z,t=0)$, we can now also directly calculate:

$$\begin{array}{r}\begin{array}{rl}a(k)& =\frac{1}{2\pi }\int dz{e}^{-ikz}A(z)\\ & =\frac{1}{2\pi }\int dz{e}^{-i(k-k_0)z}{e}^{-z^2/2{\sigma }^2}\end{array}\end{array}$$

This is a Gaussian integral of the type $\int dz{e}^{-z^2}=\sqrt{\pi }$. We will rewrite:

$$i(k-k_0)z+z^2/2{\sigma }^2=\frac{{[z+i(k-k_0){\sigma }^2]}^2}{2{\sigma }^2}+\frac{(k-k_0{)}^2{\sigma }^2}{2}$$

We can now shift the limits of the integral to obtain:

$$\begin{array}{rl}a(k)& =\frac{1}{2\pi }{e}^{-\frac{(k-k_0{)}^2{\sigma }^2}{2}}\int dz{e}^{-\frac{z^2}{2{\sigma }^2}}\end{array}$$

Changing the variable of integration to $z^{\prime }=\frac{z}{\sqrt{2}\sigma }$, we end up with the integral:

$$\begin{array}{r}\begin{array}{rl}a(k)& =\frac{\sqrt{2}\sigma }{2\pi }{e}^{-\frac{(k-k_0{)}^2{\sigma }^2}{2}}\int d{z}^{\prime }{e}^{-z^{\prime 2}}\\ & =\frac{\sigma }{\sqrt{2\pi }}{e}^{-\frac{(k-k_0{)}^2{\sigma }^2}{2}}\end{array}\end{array}$$

It is Gaussian centered around $k_c$ and of width ${\sigma }_k=\frac{1}{\sigma }$

Nk = 512;
klin = k0 + np.linspace(-4/sigmaz, 4/sigmaz, Nk);
ak = sigmaz/np.sqrt(2*np.pi)*np.exp(-sigmaz**2/2*(klin-k0)**2)

f, ax = plt.subplots()
ax.plot(klin, ak);
ax.set_xlabel('wave vector $k$ [1/L]');
ax.set_ylabel(' $a(k)$');

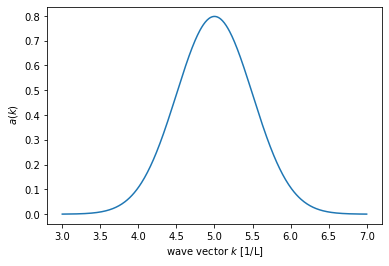
Time evolution in k space

We are now ready to simply calculate the time evolution of the wave package in k space. It is given by:

$$a(k,t)=\frac{\sigma }{\sqrt{2\pi }}{e}^{-\frac{{\sigma }^2}{2}(k-k_0{)}^2}{e}^{-i[k_0{v}_p+(k-k_0)v_g+\frac{\mathrm{\Gamma }}{2}(k-k_0{)}^2]t}$$

Quite importantly it remains a Gaussian in $k$, but only we complex numbers. Ordering in polynoms of k, we have:

$$a(k,t)=\frac{\sigma }{\sqrt{2\pi }}{e}^{-\frac{{\sigma }^2-i\mathrm{\Gamma }t}{2}(k-k_0{)}^2}{e}^{-i[k_0{v}_p+(k-k_0)v_g]t}$$

# parameters of the dispersion relation. You can set them freely
vp = 1
vg = 0.5
gamma = 1

#time
tmax = 10; Nt = 100;

tlin = np.linspace(0, tmax, Nt)
ks, ts = np.meshgrid(klin, tlin);

# the dispersion relationship
omegak = k0*vp+(ks-k0)*vg+gamma/2*(ks-k0)**2
aks = sigmaz/np.sqrt(2*np.pi)*np.exp(-sigmaz**2/2*(ks-k0)**2)

akt = ak*np.exp(-1j*omegak*ts);

f, ax = plt.subplots()
im1 = ax.pcolormesh(ts, ks, akt.real, cmap = 'bwr')
ax.set_xlabel('time $t$')
ax.set_ylabel('wavevector $k$')
ax.set_title('time evolution in k space')
f.colorbar(im1)

<matplotlib.colorbar.Colorbar at 0x10f620670>

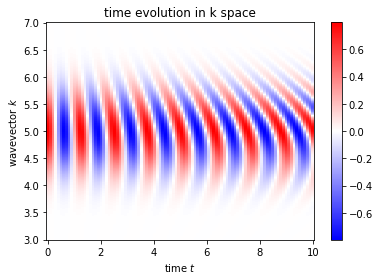
Time evolution in real space

We have now everything assembled together to calculate the time evolution in real space:

$$A(z,t)=\int dk{e}^{ikz}a(k,t)$$

Given the nice form of $a(k,t)$, we can already read it off:

• The width will be the inverse of ${\sigma }_x=\frac{1}{\sqrt{{\sigma }^2-i\mathrm{\Gamma }t}}$

• It is centered around $v_{g}t$

• It has some complicafted phase prefactor, which we will simply ignore here.

We then obtain:

$$A(z,t)\propto e^{-\frac{(z-v_{g}t{)}^2}{2({\sigma }^2-i\mathrm{\Gamma }t)}}$$

To make it simpler to understand we rewrite:

$$\frac{1}{{\sigma }^2-i\mathrm{\Gamma }t}=\frac{{\sigma }^2+i\mathrm{\Gamma }t}{{\sigma }^4+{\mathrm{\Gamma }}^2{t}^2}$$

The wave function has then the following form:

$$A(z,t)\propto e^{-\frac{(z-v_{g}t{)}^2}{2({\sigma }^4+{\mathrm{\Gamma }}^2{t}^2)}({\sigma }^2+i\mathrm{\Gamma }t)}$$

This is a Gaussian that is centered at $z=v_{g}t$ with envelope:

$${\sigma }_x^2(t)={\sigma }^2+{\mathrm{\Gamma }}^2{t}^2/{\sigma }^2$$

zs, ts = np.meshgrid(zlin, tlin);

# the dispersion relationship
sigmat_sq = sigmaz**2+gamma**2*ts**2/sigmaz**2

azt = np.exp(-(zs-vg*ts)**2/2/sigmat_sq);

f, ax = plt.subplots()
im1 = ax.pcolormesh(ts, zs, azt, cmap = 'Blues')
ax.set_xlabel('time $t$')
ax.set_ylabel('position $z$')
ax.set_title('time evolution in real space')
f.colorbar(im1)

<matplotlib.colorbar.Colorbar at 0x10f6f4b20>

previous

Numerical tests in python